Chapter 3 Flow

3.1 Overview

Flow Cytometry is a common technique employed in the field of immunology that quantifies characteristics of individual cells. Early flow cytometer designs date back to the first of half of the 20th century and while it wasn’t until the late 1960’s that the predecessors of modern fluorescence-based flow cytometers were first patented, the basic principles of these instruments have not changed in the intervening 50 years until today (Givan 2010). They operate by passing single cells through a sheath fluid that arranges them in a single file order and then into an interrogation point (often at a rate of thousands of cells per second or more) where visible light from lasers excite antibody-bound fluorophores or fluorescent dyes specific to chemicals, usually proteins, on or within each cell.

The data collected from a flow cytometer for each cell includes measurements for forward scatter (FSC), side scatter (SSC), and fluorescent marker intensities. The first two of these, FSC and SSC, are briefly explained in 3.1 (Rowley 2012) and measure morphological properties of cells while fluorescent intensities are the focus of the remaining analysis in this chapter. This analysis will also focus on several other key concerns in working with flow cytometry data like compensation, transformation, and automation through the use of several related Bioconductor packages. Most of these packages make use of flowCore (Hahne et al. 2009) and while some of the details of its utilization will be explained, it’s probably worth giving the vignette a quick browse before going further since some familiarity of FCS files, flowFrame constructs, and GatingHierarchy semantics will be assumed (though much of this is pretty intuitive given working R knowledge).

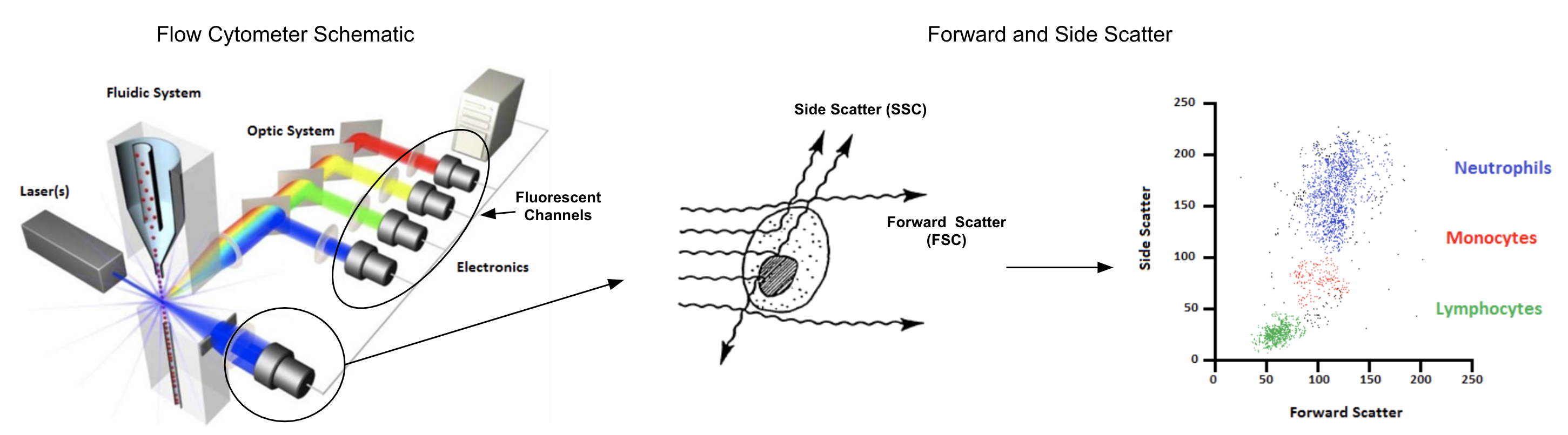
Forward and side scatter measure cell size and internal complexity, both of which are useful for QA purposes and cell type identification

Figure 3.1: Forward and side scatter measure cell size and internal complexity, both of which are useful for QA purposes and cell type identification

For more references on flow cytometry analysis and applications, see:

3.2 Exploring FlowRepository

While many sources of public flow cytometry data exist, the subject of this chapter will be experiments uploaded to FlowRepository. Specifically, the FlowRepositoryR package will be used to download two datasets related to “Optimized Multicolor Immunophenotyping Panels” (OMIP) publications. These panels consist of dyes and antibodies used to label samples relevant for one specific experimental purpose such as characterizing natural killer cell populations or chemokine expression on helper T cells.

Data available from these publications may be found in FlowRepository simply by searching for studies containing the keywork “OMIP”. Using the FlowRepository site is generally the simplest way to find relevant studies but programmatic access can also be helpful for doing more targeted searches such as for studies that have an associated FlowJo workspace, as shown below.

id name panel
FR-FCM-ZZ2T OMIP-016: Characterization of Antigen-Responsive macaque and human T-cells (Figure 1) 16
FR-FCM-ZZ2V OMIP-016: Characterization of Antigen-Responsive macaque and human T-cells (Suppl Figure 9) 16
FR-FCM-ZZ3Y OMIP-016: Characterization of Antigen-Responsive macaque and human T-cells (Online Fig 7&8) 16
FR-FCM-ZZ3Z OMIP-016: Characterization of Antigen-Responsive macaque and human T-cells (Online Figure 6) 16
FR-FCM-ZZ36 OMIP-018: Phenotyping with Chemokine Receptors 18
FR-FCM-ZZ74 OMIP-023: 10-Color, 13 antibody panel for in-depth phenotyping of human peripheral blood leukocytes 23
FR-FCM-ZZK4 OMIP-028: Rhesus macaque NK cell subset 28
FR-FCM-ZZWU OMIP-030: Characterization of eight major human CD4+ T helper subsets, including Tregs, via surface markers 30
FR-FCM-ZZX9 OMIP-035: Nonhuman Primate NK cell functional assay 35
FR-FCM-ZYY6 OMIP-039: Detection and analysis of human adaptive NKG2C+ natural killer cells 39
FR-FCM-ZYBP OMIP-043: Identification of Human Antibody Secreting subsets 43

3.3 Tools

TODO:

  • Intro openCyto and flowWorkspace
  • Explain how R tools are most appropriate for automated workflows (not manual gating)
  • Explain single-step automation vs whole workflow automation
  • Describe FlowJo and Cytobank

3.4 Simple Analysis Automation (OMIP-021)

Initial Example: OMIP-021: Innate-like T-cell Panel (FR-FCM-ZZ9H)

FSC-A FSC-H SSC-A SSC-H 450/50Violet-A 525/50Violet-A 540/30Violet-A 585/15Violet-A 610/20Violet-A 670/30Violet-A 670/14Red-A 730//45Red-A 780/60Red-A 530/30Blue-A 710/50Blue-A 582/15Yellow-A 610/20Yellow-A 670/30Yellow-A 710/50Yellow-A 780/60Yellow-A Time
119565 108322 82937 76142 1130 257 630 1002 3625 5465 7061 13215 6966 222.4 17786 803 418 20700 29263 19368 136
107004 77596 262143 207144 1223 732 995 169 721 114 1110 8055 2695 420.8 926 358 294 851 70563 2586 136
214908 139281 262143 226353 3218 1049 2240 1467 7903 10092 8914 26039 10930 561.1 19171 994 733 21668 88813 12031 136
119453 107496 67842 62072 2473 351 5828 14664 22003 3548 7316 6115 951 112.0 5504 184 448 4450 17505 1143 136
122345 111352 62728 56540 541 194 2601 735 1267 1095 3060 4466 4531 95.4 5793 435 440 8354 16969 3564 137
137030 124521 77133 70557 4062 471 10052 23228 41648 6317 13904 15326 2217 152.7 5801 189 829 10039 21626 2003 138
153801 122139 122174 80251 924 735 2110 1059 2827 2641 287 1277 611 4595.7 6182 175 201 822 33043 1301 138
177071 145150 168704 148426 731 679 1243 337 1045 201 415 9995 1659 291.3 1052 271 366 570 47515 953 138
165853 118245 122113 89253 2785 511 7996 2560 15636 9627 10654 29089 14198 337.8 20733 1203 2341 24269 40187 12859 138
121005 108937 72537 66157 255 205 3215 724 2316 153 361 829 141 166.0 4320 335 819 1027 21945 244 138

In this dataset, one way to identify lymphocytes is by looking at modes in the relationship between side and forward scatter:

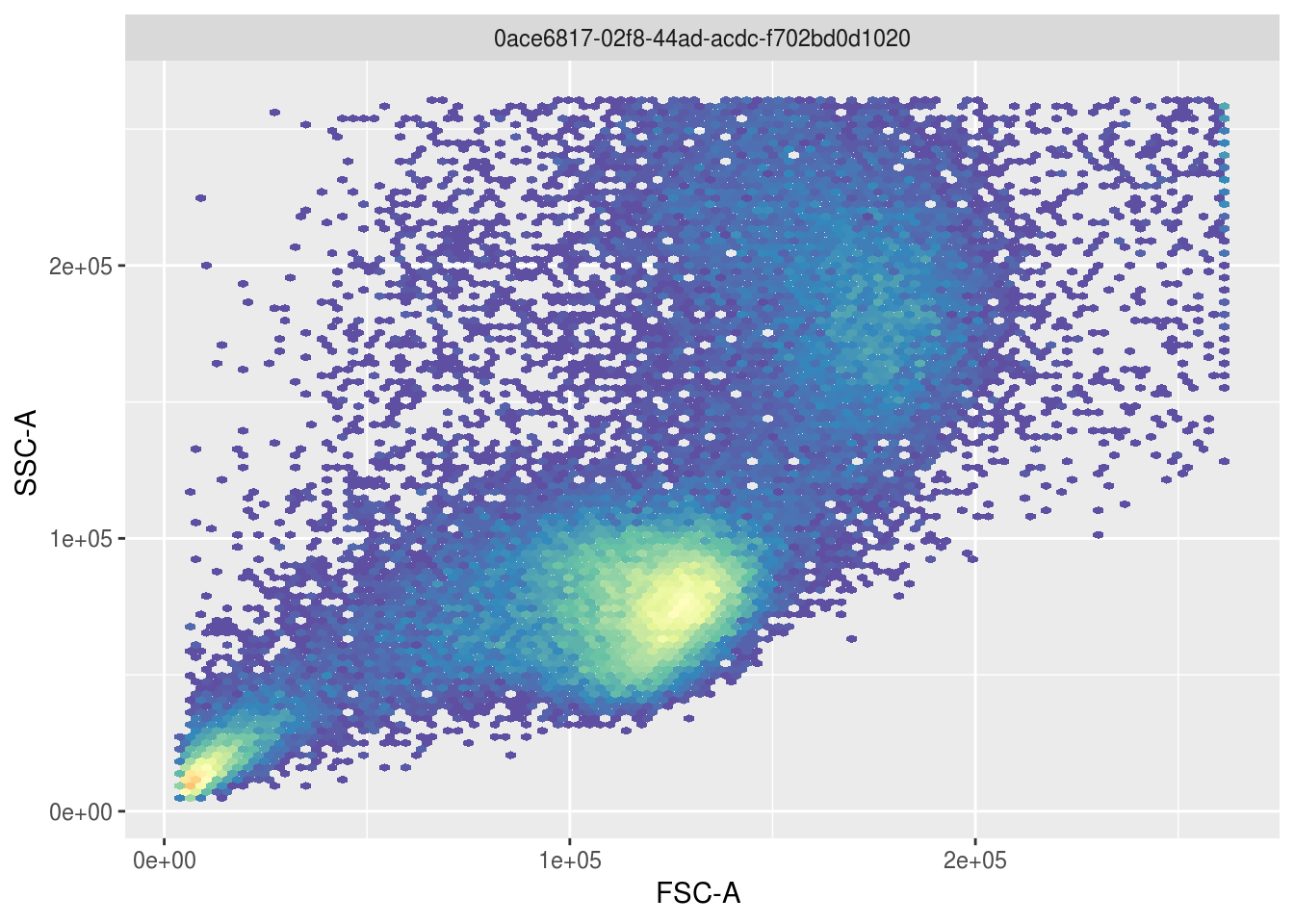
To identify the lymphocyte cells above, openCyto gating can be used to select the largest cluster of cells automatically and visualize what fraction of the population these cells constitute:

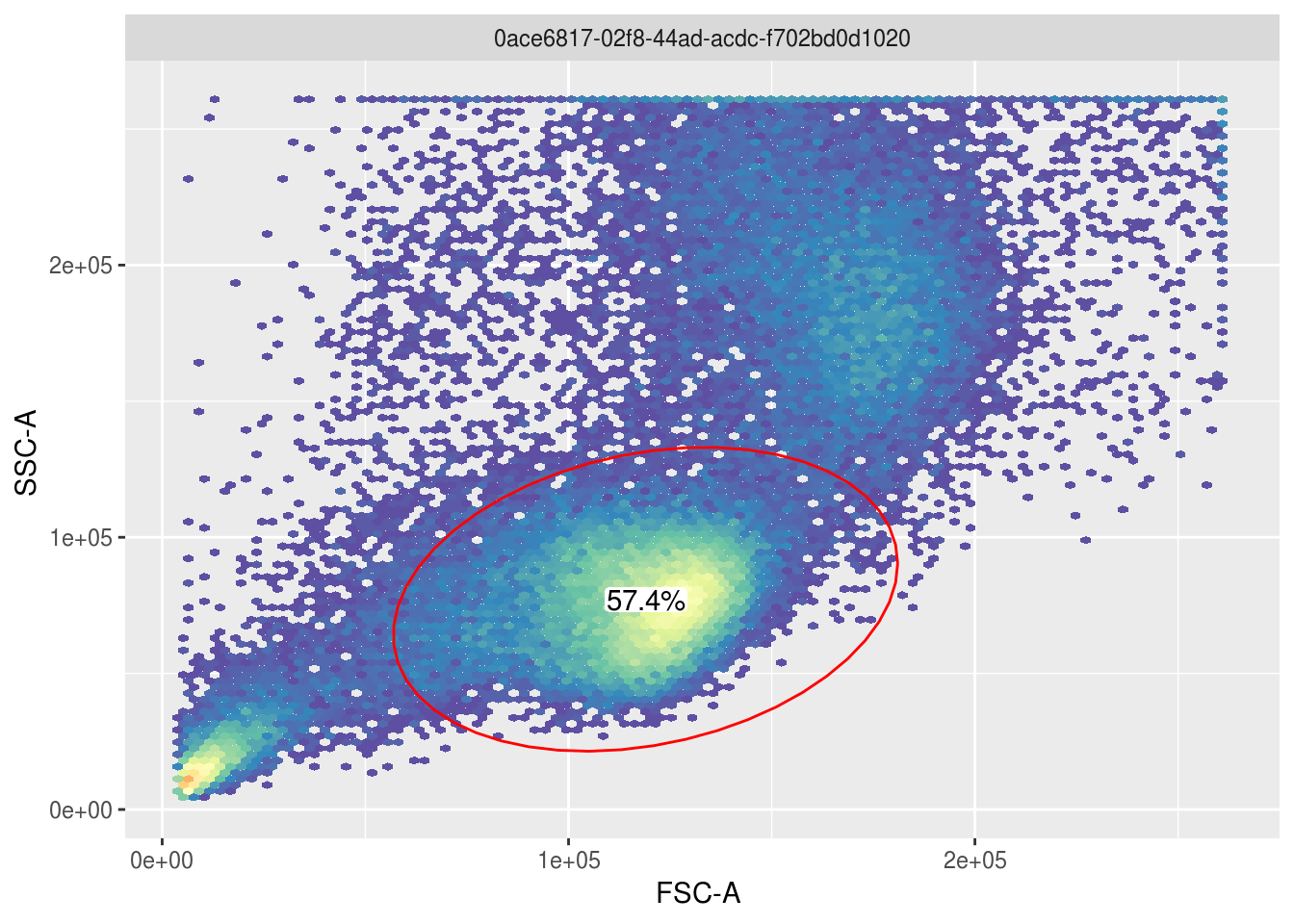
3.4.1 Gating

By repeating the above process for all cell types of interest in the paper, the workflow can be reproduced via a GatingTemplate as shown below, which could also be built programmatically instead. The graphical representation of the template shows how cell types will be recursively defined based on 2 dimensional filters:

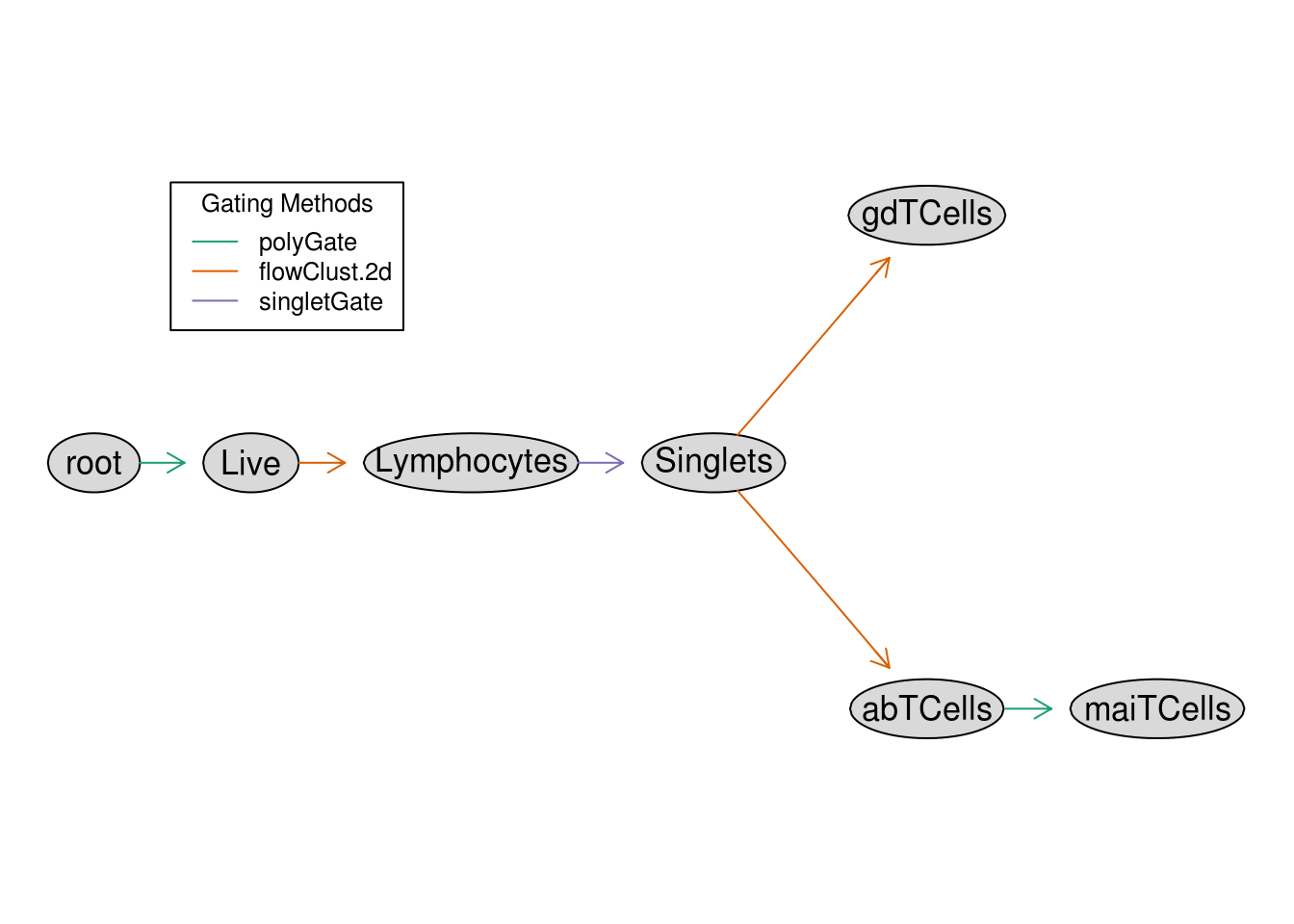
The above template only outlines the gating workflow but to apply it to our data, these are the common steps:

  • Apply compensation to the raw FCS data if necessary (not necessary in this case as the authors did this beforehand)
  • Define channel transformations to make gating and visualization possible
  • Define any custom gating functions needed in the workflow, which is particularly useful for setting manual gates
  • Apply the gating template to the data at hand, which in this case is represented as a flowFrame but could also be a flowSet representing a collection of experiments

Here is the realization of these steps for this data specifically:

3.4.2 Results

Now that the workflow is finished, here is a look at all cell types identified:

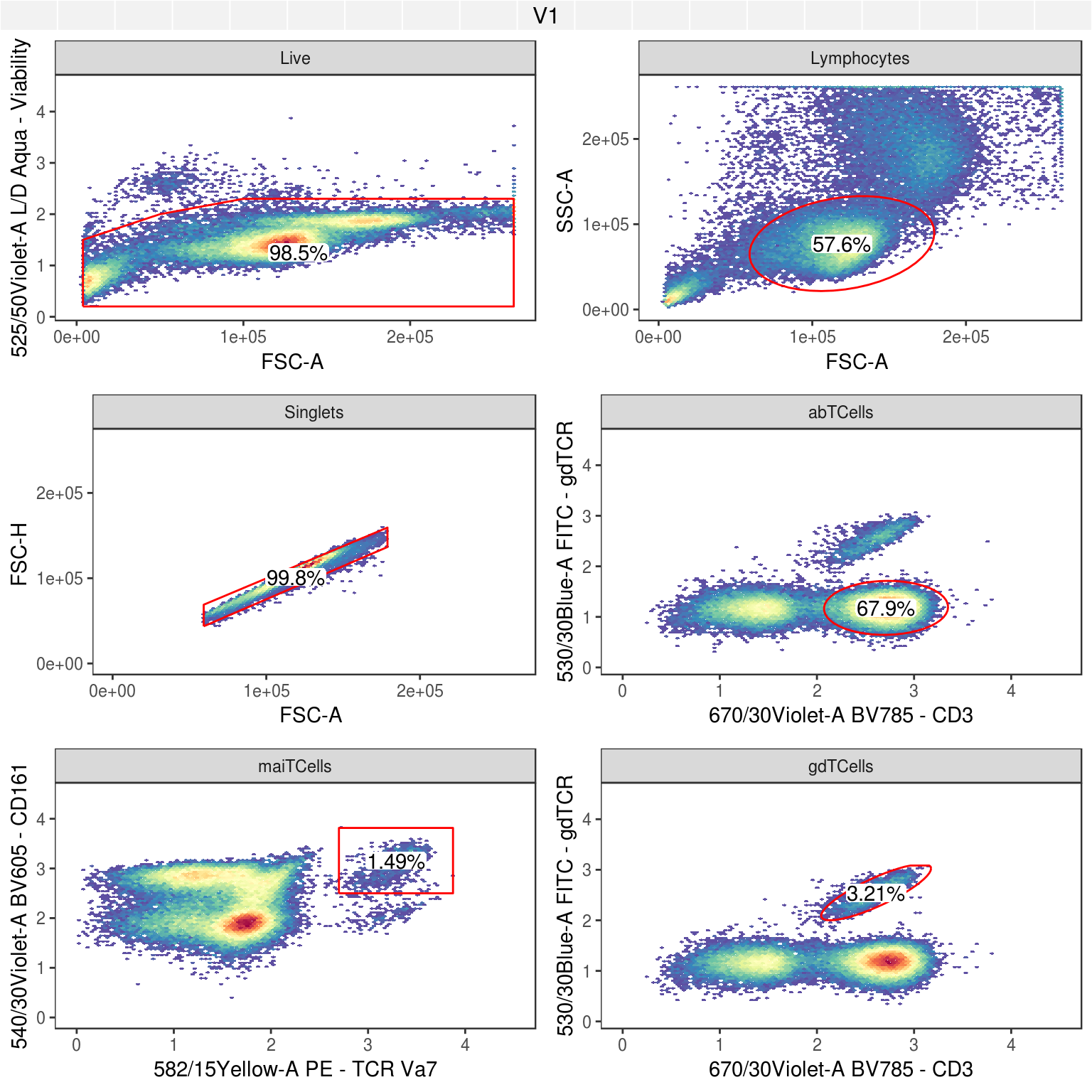
This should then be comparable to what was in the OMIP-021 publication, and here are relevant figures demonstrating the similarity of the cell subsets captured:

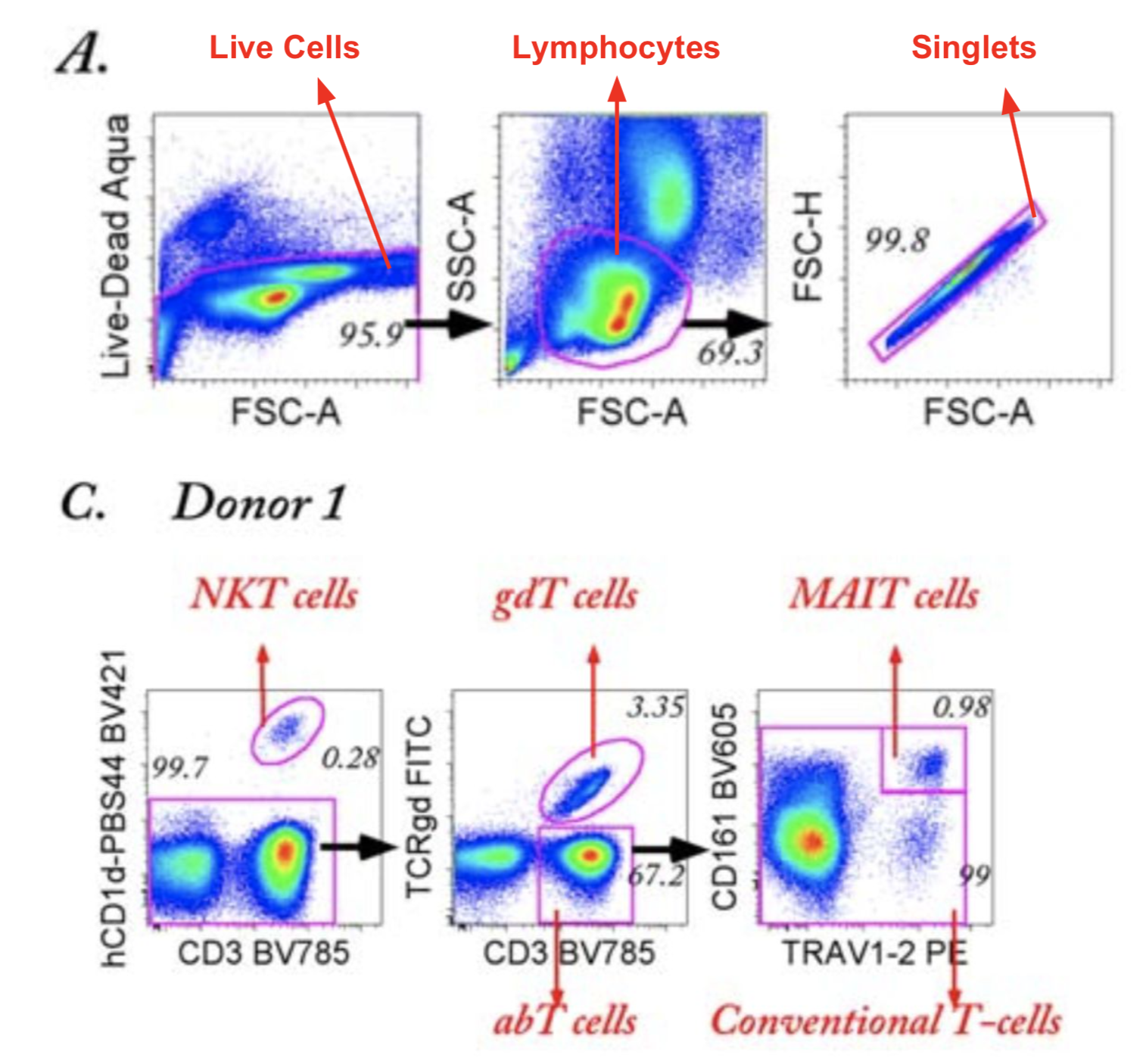
Gating strategy illustrated with annotated figures from OMIP-021

Figure 3.2: Gating strategy illustrated with annotated figures from OMIP-021

3.5 Advanced Analysis Automation (OMIP-030)

Advanced Example: OMIP-030: Characterization of eight major human CD4+ T helper subsets, including Tregs, via surface markers (FR-FCM-ZZWU)

3.5.1 Gating

Load a flow workspace, which will contain all gaiting and cell expression information:

Show the correspondence between the flow cytometer channels and the marker names in the panel.

name desc
$P1 FSC_A NA
$P2 FSC_W NA
$P3 SSC_A NA
$P4 SSC_W NA
$P5 Comp-LIVE_DEAD_BLUE_A L+D
$P6 Comp-BRILLIANT_VIOLET_421_A CD38
$P7 Comp-V500_A CD4
$P8 Comp-BV_570_A CD45RA
$P9 Comp-QDOT_605_A CD3
$P10 Comp-QDOT_655_A CD8
$P11 Comp-BV_711_A CD25
$P12 Comp-BV_785_A CD196
$P13 Comp-FITC_A CD183
$P14 Comp-PER_CP_E_FLUOR_710_A CD161
$P15 Comp-PE_A CD194
$P16 Comp-PE_TEXAS_RED_A CD197
$P17 Comp-PE_CY5_5_A CD20
$P18 Comp-PE_CY7_A CD185-bio
$P19 Comp-APC_A CCR10
$P20 Comp-ALEXA_FLUOR_700_A Ki67
$P21 Comp-APC_CY7_A CD127
$P22 TIME NA

Plot the gating workflow starting from where T Cells are first identified:

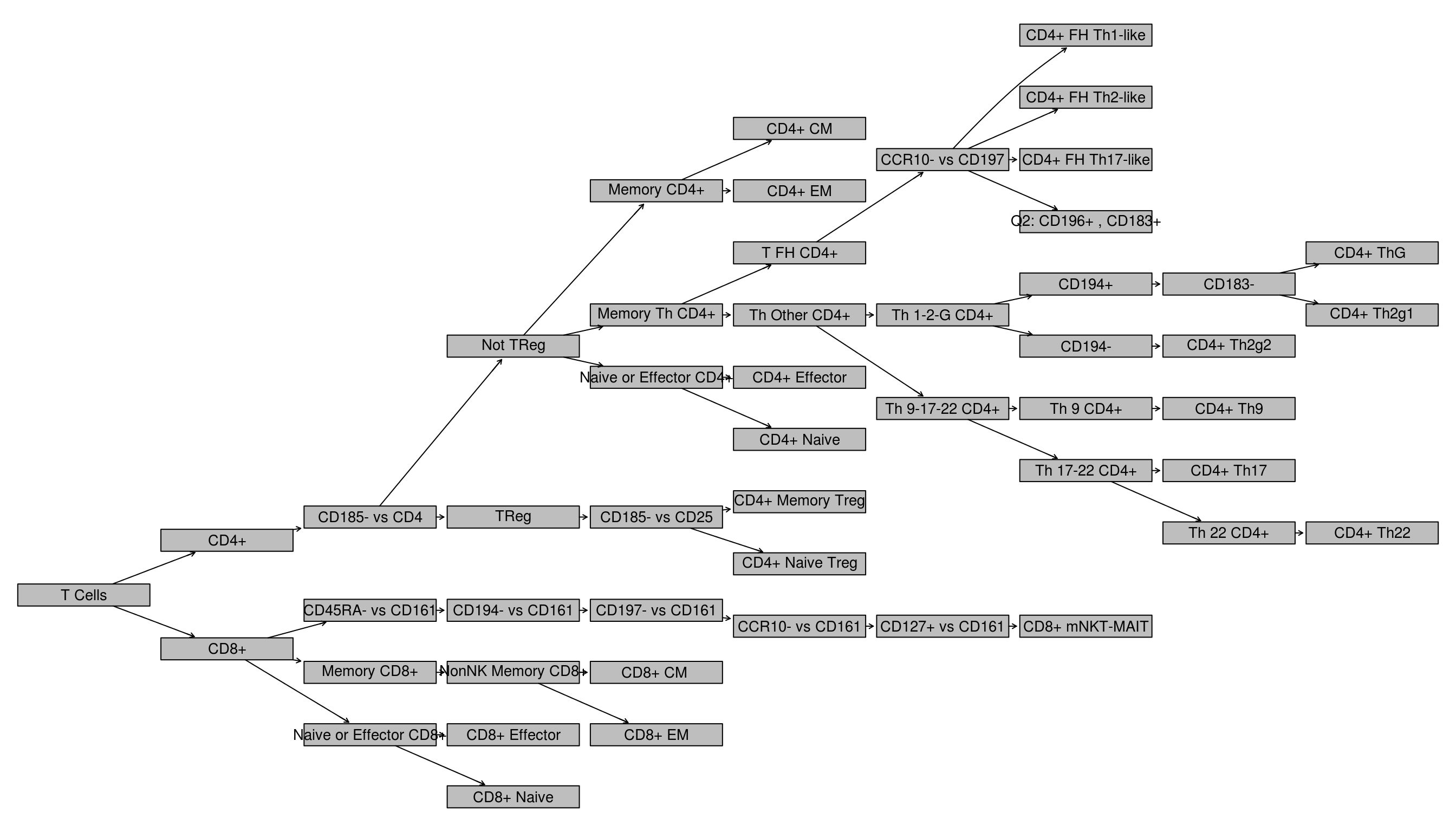
TODO: Explain gating via differentiation model

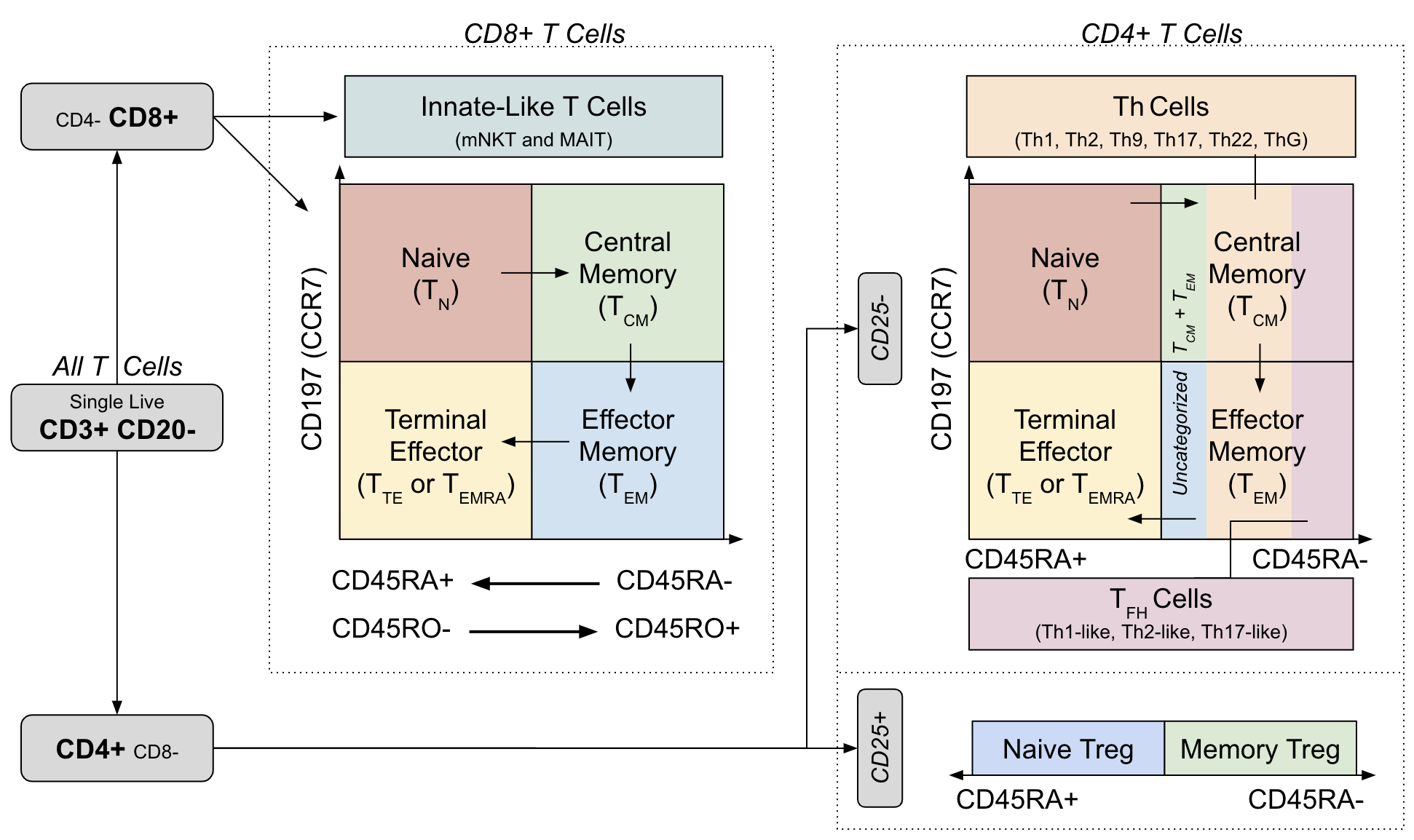
Gating strategy and cell differentiation overlay from OMIP-030

Figure 3.3: Gating strategy and cell differentiation overlay from OMIP-030

3.5.2 Extracting Single Cell Data

Identify terminal nodes (i.e. cell populations) in the workflow which were, by convention, prefixed with either CD4+ or CD8+ and then use those nodes to extract single-cell data into a data frame (useful for custom visualizations).

TODO: make display of pop names better (and make states a map from type?)

population state class
CD4+ CM CM CD4+
CD4+ EM EM CD4+
CD4+ FH Th1-like NA CD4+
CD4+ FH Th2-like NA CD4+
CD4+ FH Th17-like NA CD4+
CD4+ ThG NA CD4+
CD4+ Th2g1 NA CD4+
CD4+ Th2g2 NA CD4+
CD4+ Th9 NA CD4+
CD4+ Th17 NA CD4+
CD4+ Th22 NA CD4+
CD4+ Effector EMRA CD4+
CD4+ Naive Naive CD4+
CD4+ Memory Treg NA CD4+
CD4+ Naive Treg NA CD4+
CD8+ mNKT-MAIT NA CD8+
CD8+ CM CM CD8+
CD8+ EM EM CD8+
CD8+ Effector EMRA CD8+
CD8+ Naive Naive CD8+

Next, extract data from the flowFrame using the getIndices function which, for a given list of m node names, returns an n x m matrix where n is the number of cells and m logical columns contain TRUE/FALSE values indicating whether or not the cell (row) was in that population.

type state class label CD3 CD4 CD8
CD8+ Naive Naive CD8+ Naive 145.1010 74.11814 171.20775
CD8+ Naive Naive CD8+ Naive 160.1456 55.52768 167.54243
CD8+ Naive Naive CD8+ Naive 150.9526 97.35362 170.99518
CD8+ Effector EMRA CD8+ Effector 128.7182 103.24777 171.34473
CD4+ Th1 CM CD4+ Th1 163.2715 168.34281 52.61338
CD4+ Naive Naive CD4+ Naive 172.3580 171.73494 71.21534
CD4+ Th17 EM CD4+ Th17 138.2115 159.26622 50.87339
CD8+ CM CM CD8+ CM 130.1044 110.77394 169.39673
CD4+ Naive Naive CD4+ Naive 153.2279 167.86806 51.67805
CD8+ CM CM CD8+ CM 154.5896 90.04521 187.45023

3.5.3 Preliminary Visualization

Plot the distribution of different cell types noting that the memory state exhibited by CD4+ and CD8+ cells is considered independent of the other primary phenotypes (helper, regulatory, innate-like, etc.). For example, this means that a Th17 cell can also exhibit CM or EM cell markers so in ?? this is shown as sums of constituent cell populations for each memory state.

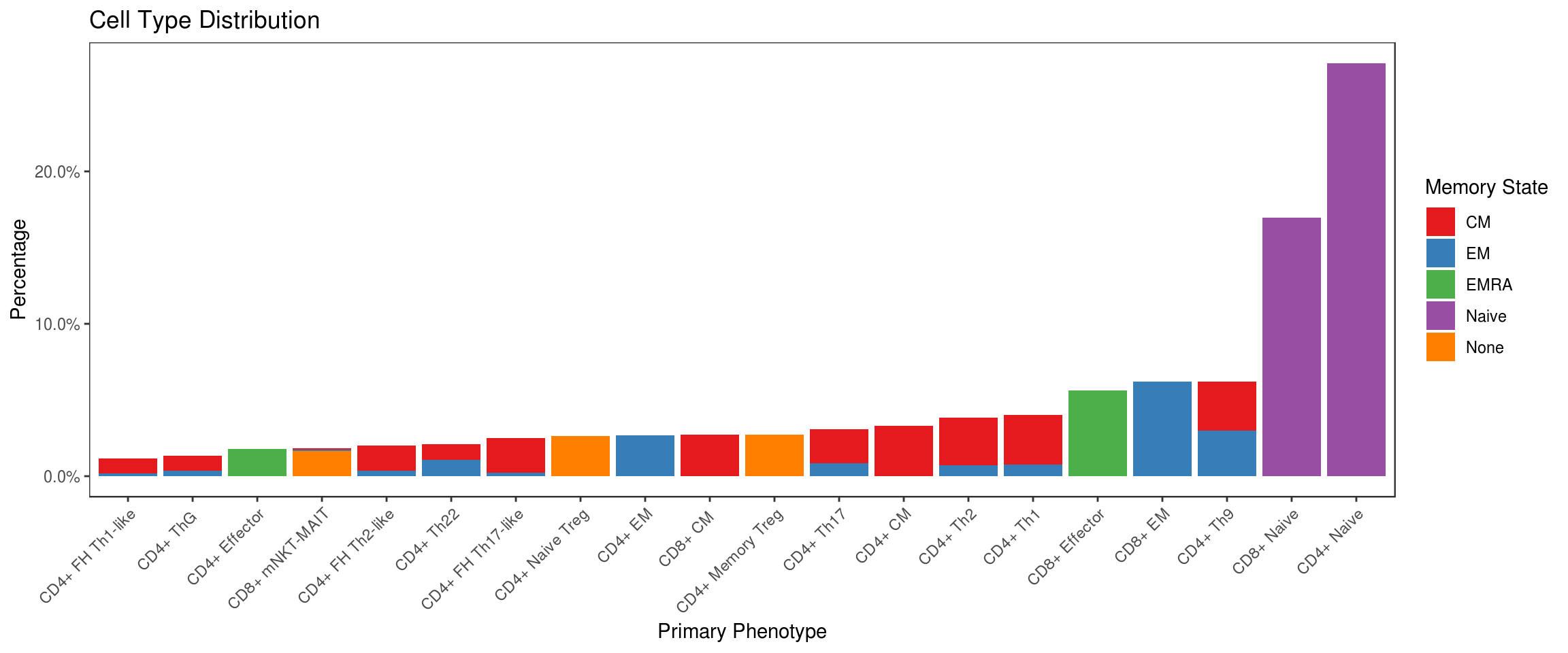
Workflow gates for terminal cell populations overlaid on relevant expression distributions:

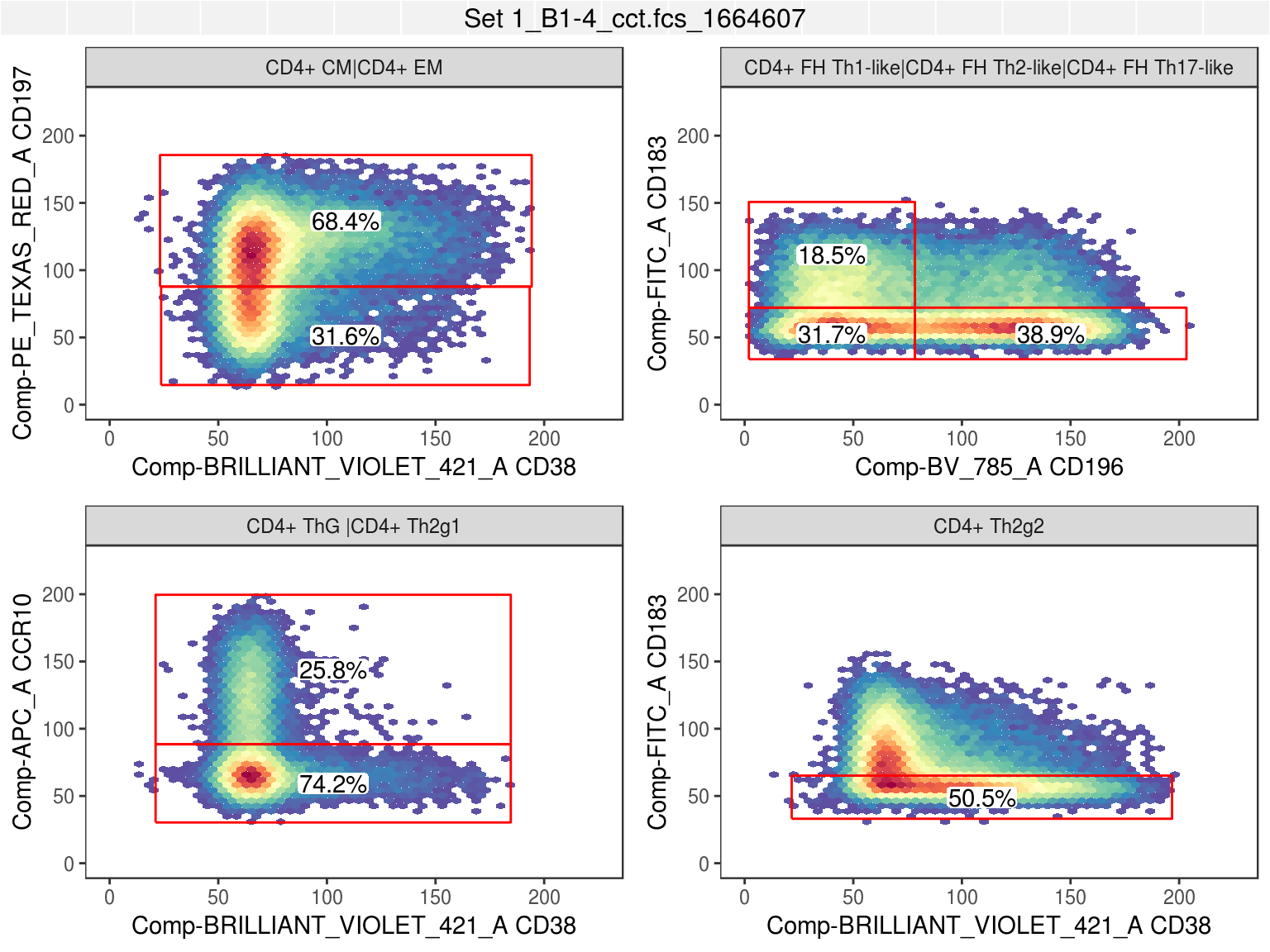
Visualize expression distribution separation for each marker and cell type using the Resolution Metric (\(R_D\)) (Bushnell 2015) (Ortyn et al. 2006), which is used here to measure the difference in median (scaled by dispersion) between the expression of a marker for one cell type vs all others.

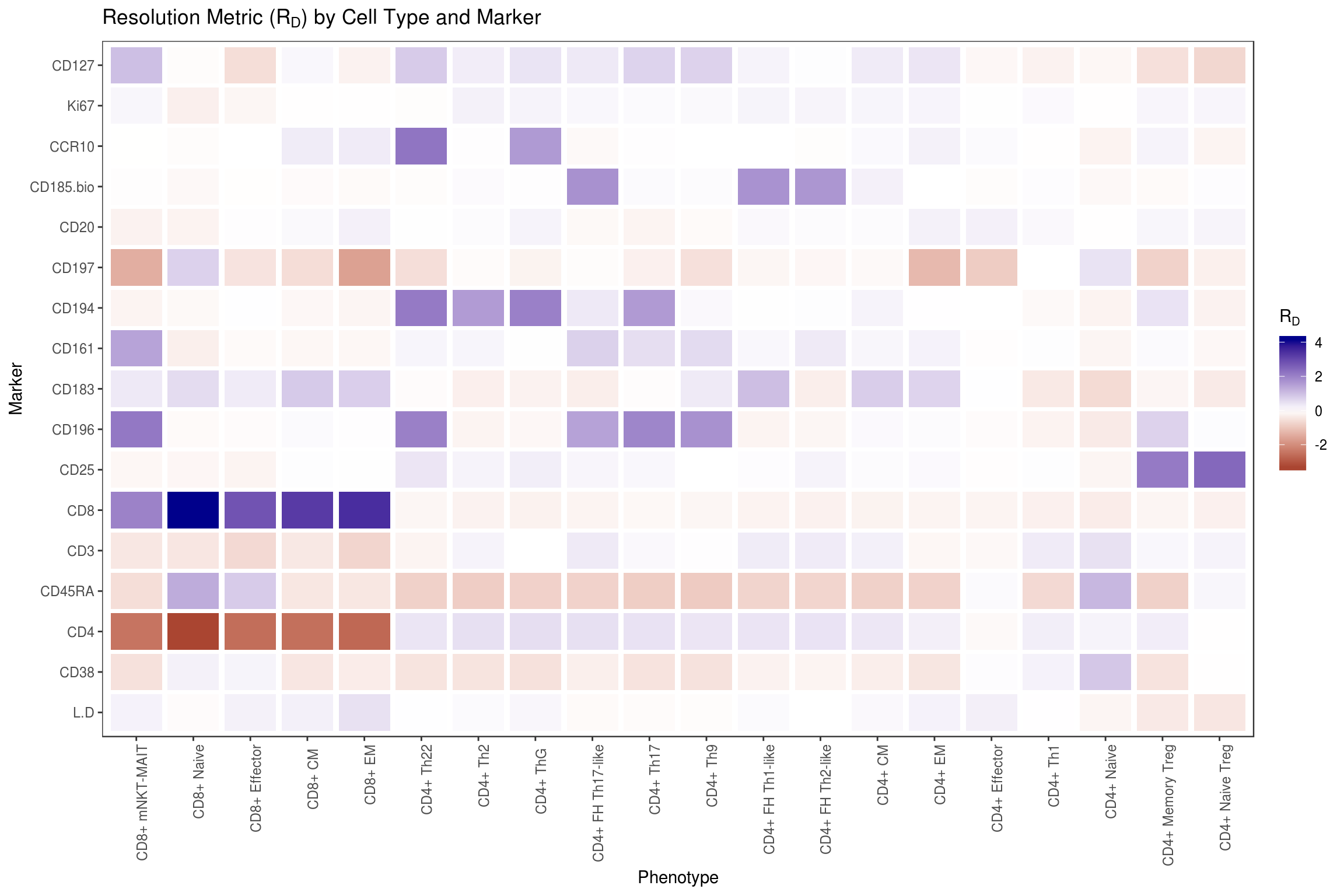
Show example distributions for individual cell type and marker pairs with low, near-zero, and high \(R_D\) values.

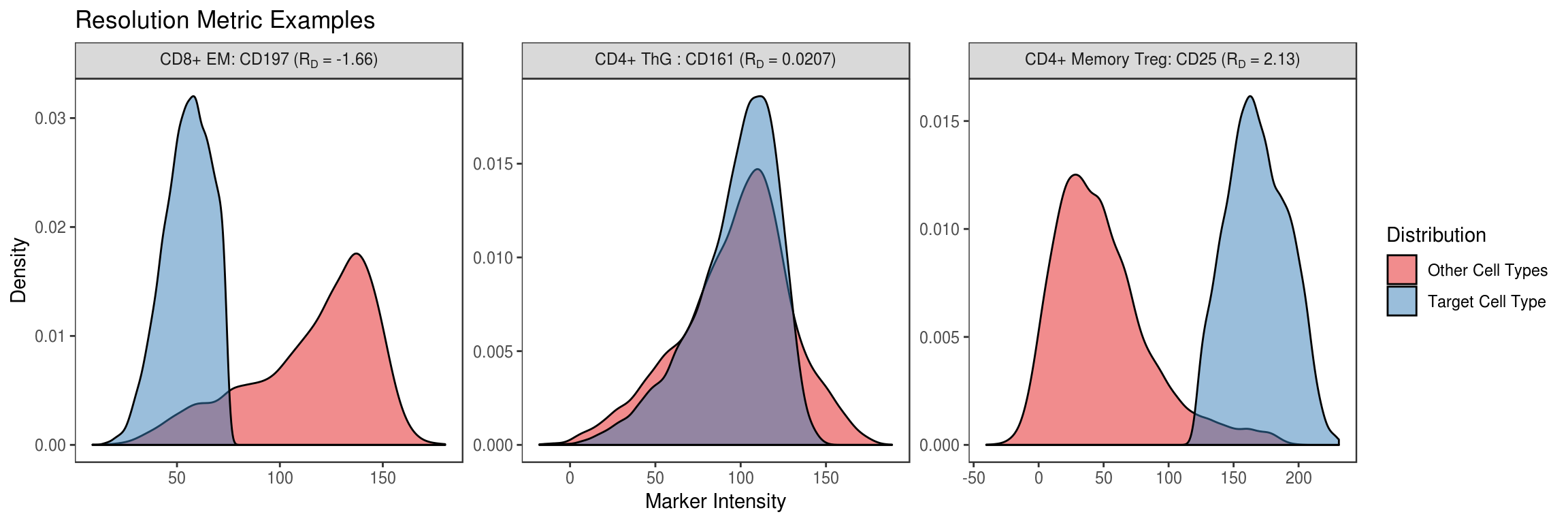
While univariate and bivariate measures of separation are useful for some cell populations, many are defined in the workflow based on combinations of several different positive and negative markers. For example, Th9 cells are defined as CCR10-, CD185-bio-, CD194- and CD196+, excluding markers to isolate T cells in the first place. This is definitely a type of cell that cannot be visualized easily based on one or two markers alone so instead, we will try a UMAP decomposition to project all fluorescent intensity measurements into a 2D space in such a way that preserves proximity between data points (cells in this case) on the manifold assumed to exist in the original high dimensional space. This manifold may not actually be two dimensional, which is often the case, but the 2D assumption will still provide results that give a sense of which cell types most readily differentiate from one another in this panel.

TODO: Compare to TSNE (runtimes and interpretation)

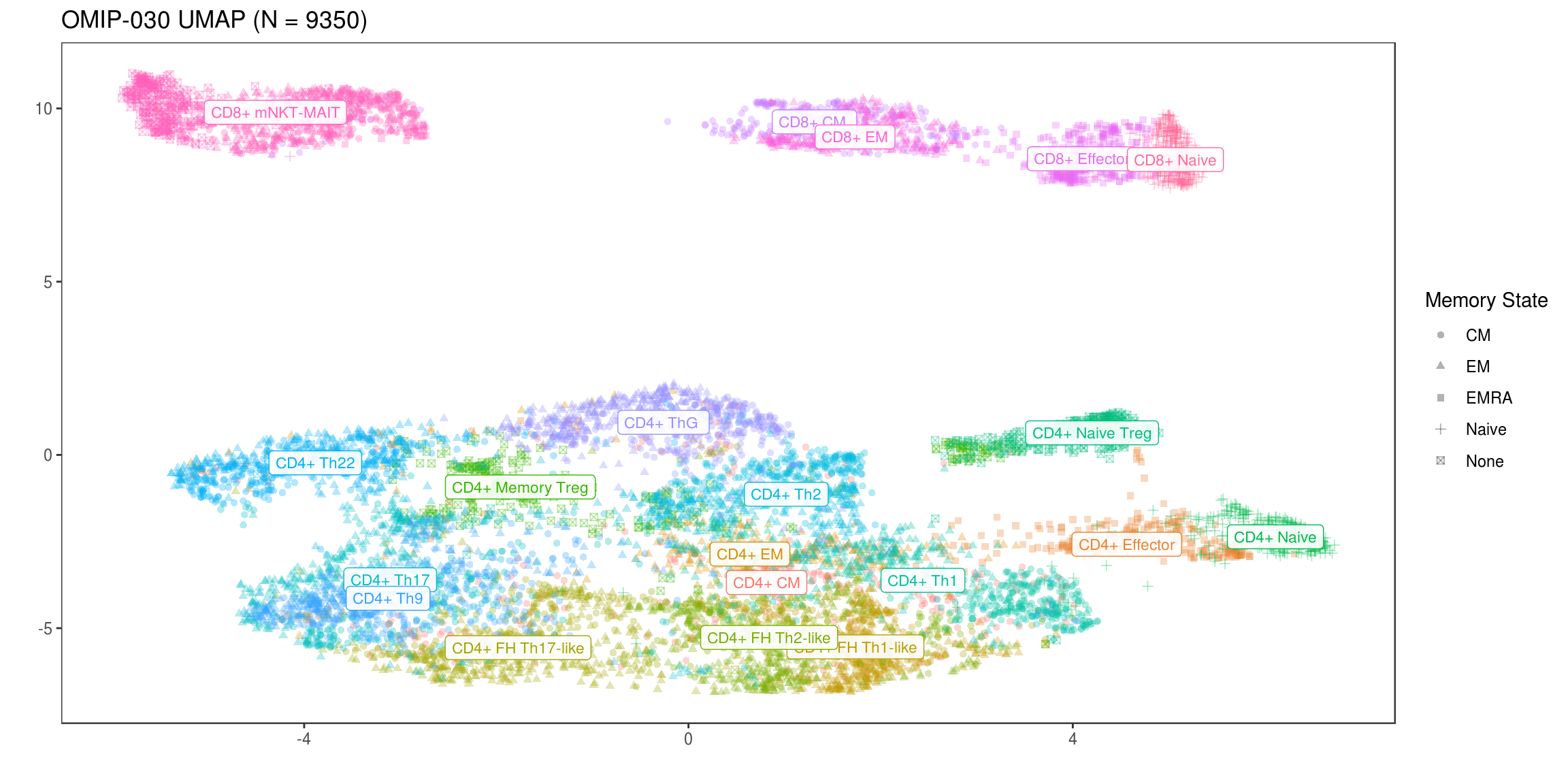
3.5.4 FlowSOM

The FlowSOM package implements an algorithm for automatic clustering and visualization of cytometry data based on self-organizing maps. Much like UMAP, this technique attempts to learn a low dimensional representation for large numbers of numerical measurements but unlike such methods used for visualization, this representation is not limited to 2 or 3 dimensions. The FlowSOM algorithm instead works by building a minimum spanning tree between clusters in the lower dimensional space, which again can have > 3 dimensions, before providing a variety of ways to interrogate the resulting graph structure. This structure also has the advantage of being able to be visualized easily in 2 dimensions through arrangement of the graph nodes into any plane that makes visualizing their connections possible.

There are a variety of similar algorithms such as SPADE, flowMeans, ACCENSE, PhenoGraph, and X-shift, but FlowSOM was chosen in this case because it offers similar or superior accuracy to all other methods while also executing much, much faster (Weber and Robinson 2016). For more information on FlowSOM, see the original publication or the Biconductor package vignette.

To use FlowSOM, the first step necessary is to decide which expression markers will be used for clustering. In this case, just as in the UMAP visualization, we want these markers to be specific to cell phenotypes but not viability or T cell isolation. FlowSOM is also built to operate well with flowCore data structures so the flowFrame containing the OMIP-030 data must also be filtered to the same cells studied thus far.

3.5.4.2 Interrogation

One way to explore the resulting cluster graph is with individual nodes represented as “Star Charts”. These charts make it possible to see over/under expression for several markers in a cluster simultaneously. However, the 14 markers used for clustering make for a cluttered presentation so 6 key markers are chosen here to make it possible to see patterns in the clusters more clearly.

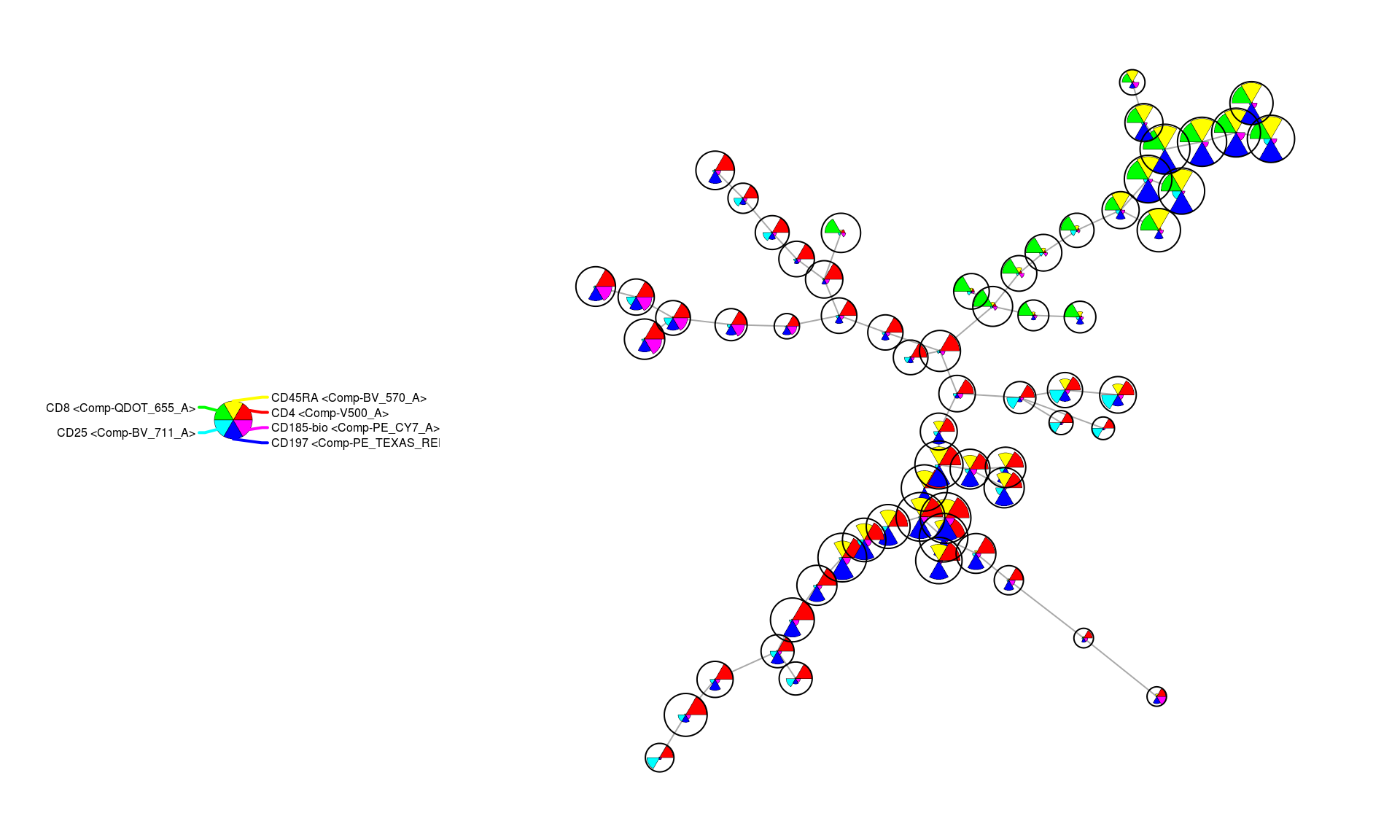
In the above figure, CD4 and CD8 over-expression roughly separate the graph into two halves (the red and green nodes). Within each of those partitions the CD197+ a.k.a. CCR7+ (blue) clusters are also evident and indicate more naive cell groups. Furthermore, within the CD4+ partition of the graph it is also clear that certain clusters have high expression levels of CD25 (cyan) as well as CD185-bio (pink) indicating higher representation from regulatory and follicular helper cells, respectively.

Given no knowledge of the cell types a priori, a useful tool for investigating this representation of our dataset further is to simply specify positive/negative rule sets for specific cell types, based on a priori biological knowledge, and visualize which clusters best match those profiles. Two examples of this are shown below with profiles defined as “queries” of the SOM MST for both \(T_{reg}\) and \(T_{FH}\) cells.

TODO: Upload and reference supplemental OMIP-030 doc containing these profiles for each cell type

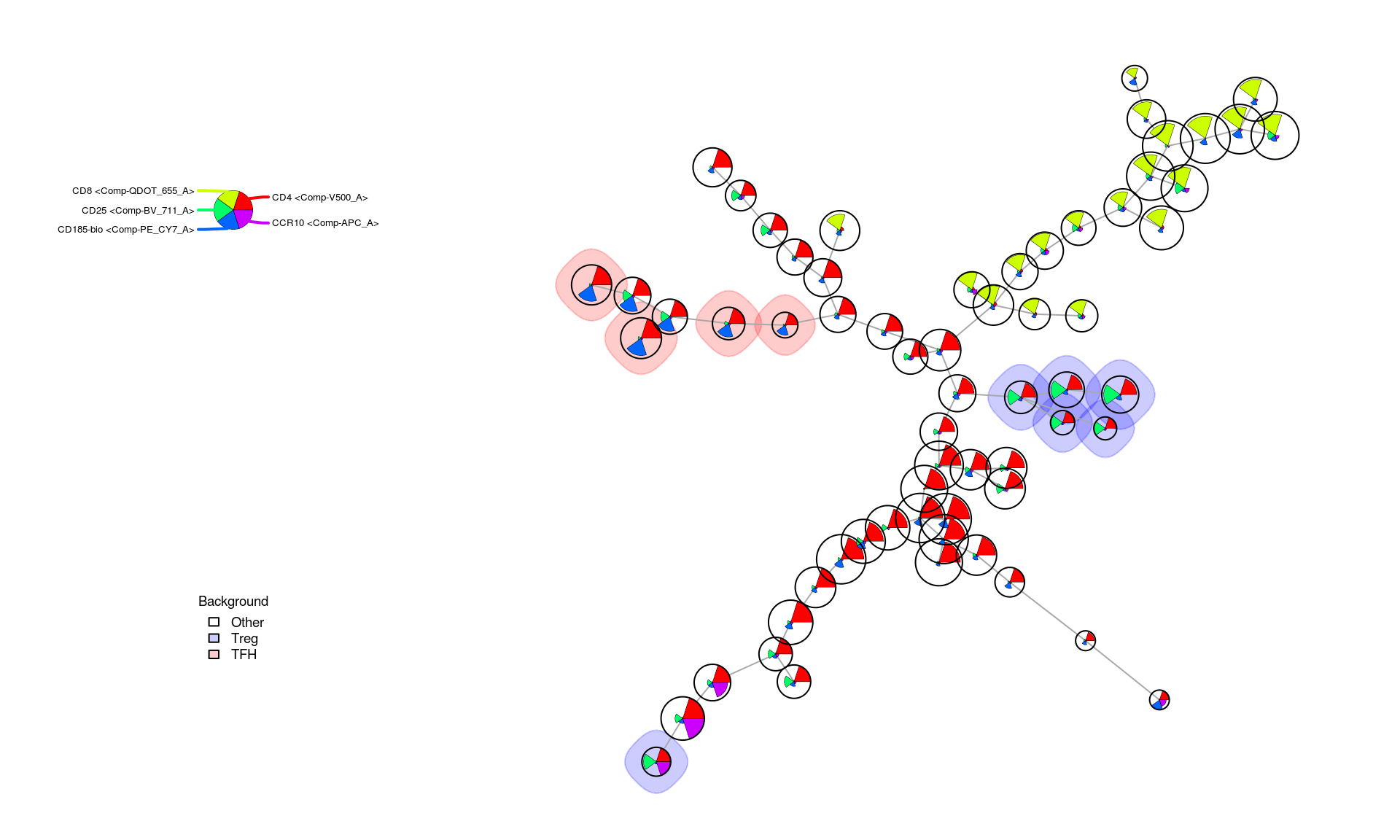
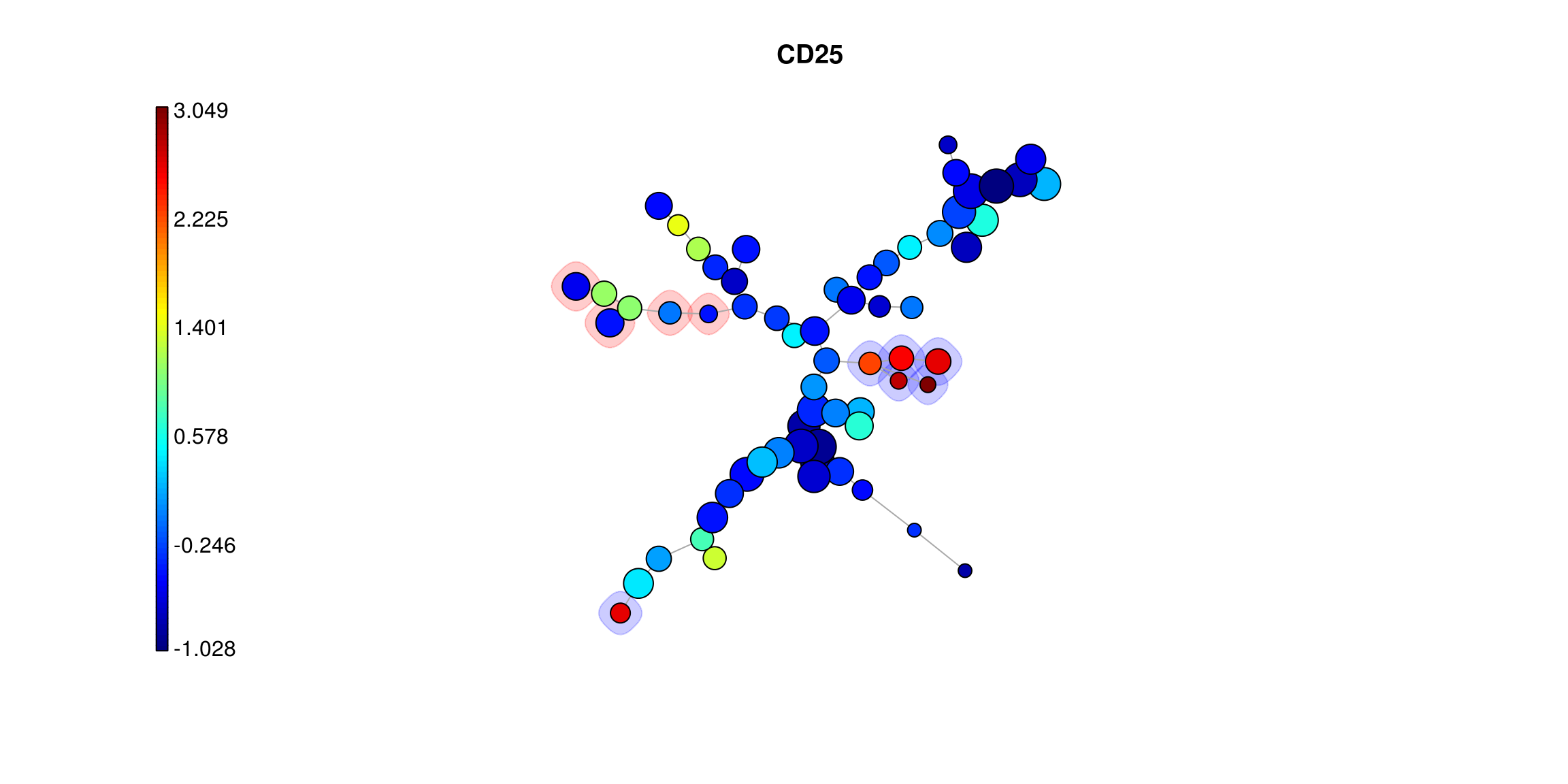
The query results above show that \(T_{reg}\) and \(T_{FH}\) likely exist within this clustered representation and that the star chart profiles indicate expression patterns we would expect from those cell types. For a more detailed view of the distribution for a marker across the clusters it is also possible to color each one based on the values of a single marker. This makes small differences betweeen clusters more apparent and can help dissambiguate those that likely represent very similar cell types from one another.

3.5.5 Results

A more empirical validation of the FlowSOM results can also be done based on comparison to the manual gating results. Below, this is done by “Meta Clustering” the SOM nodes into some number of groups close to the number of different cell types determined through the manual process. FlowSOM makes visualizing the results of this possible through pie chart visualizations where for each node, the pie represents what portion of the manually gated cell types fall within it.

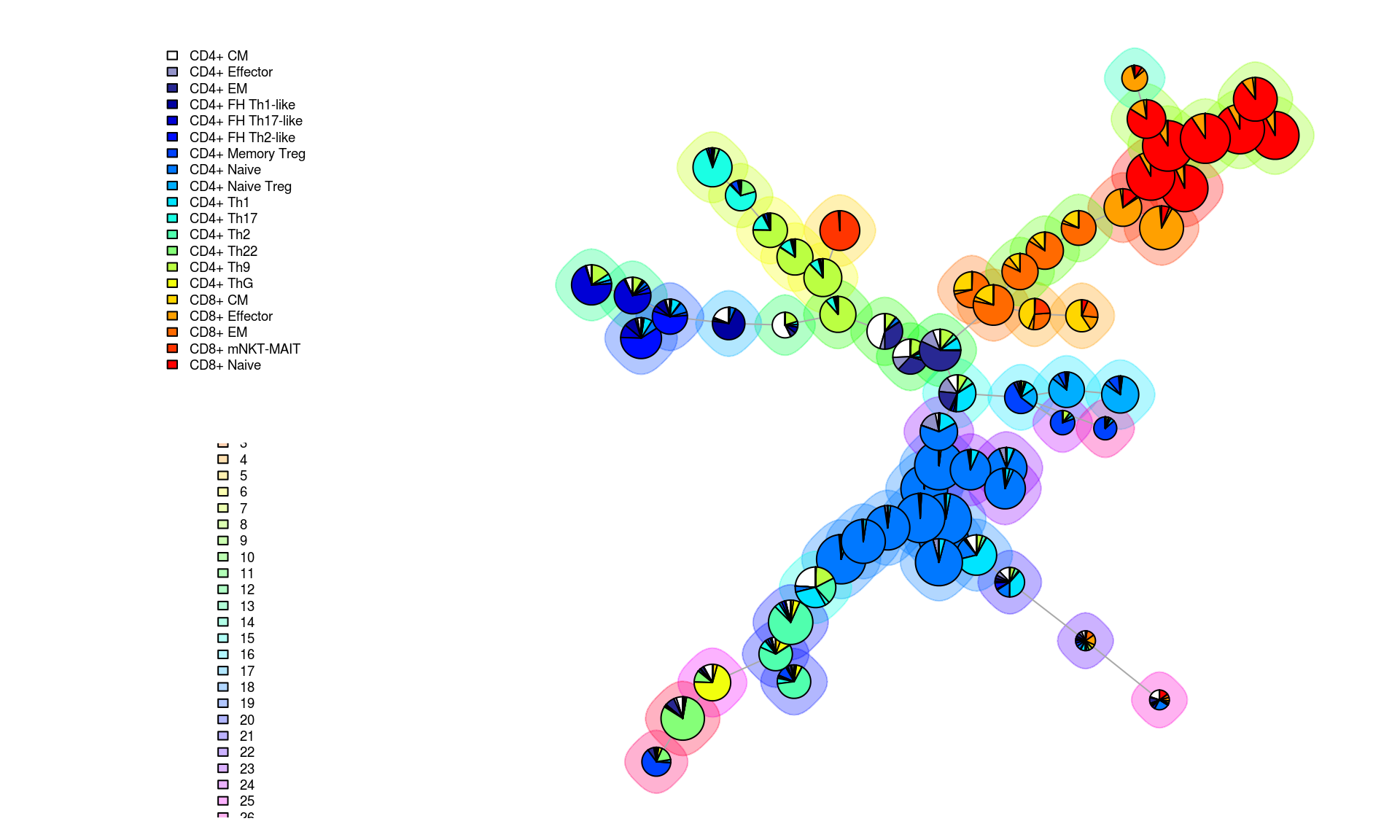
This figure demonstrates that certain nodes are dominated by one cell type (e.g. CD4+ naive and CD8+ naive) while others contain many different cell types in the manual results. It also shows that certain groups of an individual nodes can confidently be placed into less granular meta clusters (indiated by the background halos around the nodes) while for others the assignment is less convincingly related to a known cell profile.

The process for determining all of this with no manual gating information would usually involve deciding which known phenotype is most closely related to each cluster and/or meta-cluster so to continue further, this process will be emulated by electing the most common cell type from the manual gating result as the sole type for that inferred group. This then provides both a predicted and ground truth assignment for each cell which is aggregated into a comparison below showing how well the proportions of cells for each label align.

# meta_clustering = xdim*ydim length vector with meta cluster integers
# mst_som$map$mapping[,1] = Indexes of nodes (1 to xdim*ydim) for each of ~700k cells
df_cluster <- df %>% mutate(cluster=meta_clustering[mst_som$map$mapping[,1]]) %>% 
  group_by(cluster, type) %>% tally %>% ungroup %>% 
  group_by(cluster) %>% filter(n==max(n)) %>% ungroup %>% select(-n, cluster, predicted_type=type)

df_comparison <- df %>% mutate(cluster=meta_clustering[mst_som$map$mapping[,1]]) %>%
  rename(actual_type=type) %>%
  inner_join(df_cluster, by='cluster') 

df_percents <- df_comparison %>% select(predicted=predicted_type, actual=actual_type) %>% 
  rowid_to_column('id') %>% melt(id.vars=c('id'), value.name='type') %>% 
  group_by(variable, type) %>% tally %>% ungroup %>%
  group_by(variable) %>% mutate(percent=n/sum(n))

df_stats <- inner_join(
  df_percents %>% select(-n) %>% spread(variable, percent) %>% 
    rename(predicted_percent=predicted, actual_percent=actual),
  df_percents %>% select(-percent) %>% spread(variable, n) %>% 
    rename(predicted_n=predicted, actual_n=actual),
  by='type'
) 
fit <- lm(log10(actual_percent) ~ log10(predicted_percent), data=df_stats)
p_value <- format(summary(fit)$coef[2,4], digits=3)
rsq_value <- format(summary(fit)$r.squared, digits=3)

df_stats %>%
  ggplot(aes(x=predicted_percent, y=actual_percent, color=type, size=actual_n)) + 
  geom_point() + 
  geom_abline(intercept=fit$coefficients[1], slope=fit$coefficients[2]) +
  scale_x_log10(limits=c(.01, .3)) + scale_y_log10(limits=c(.01, .3)) +
  scale_size_continuous(range=c(2, 5)) +
  ggtitle(bquote(paste("Predicted vs Actual Cell Population Sizes ("*R^{2}~"="~.(rsq_value)*", p"~"="~.(p_value)*")" ))) +
  flow_theme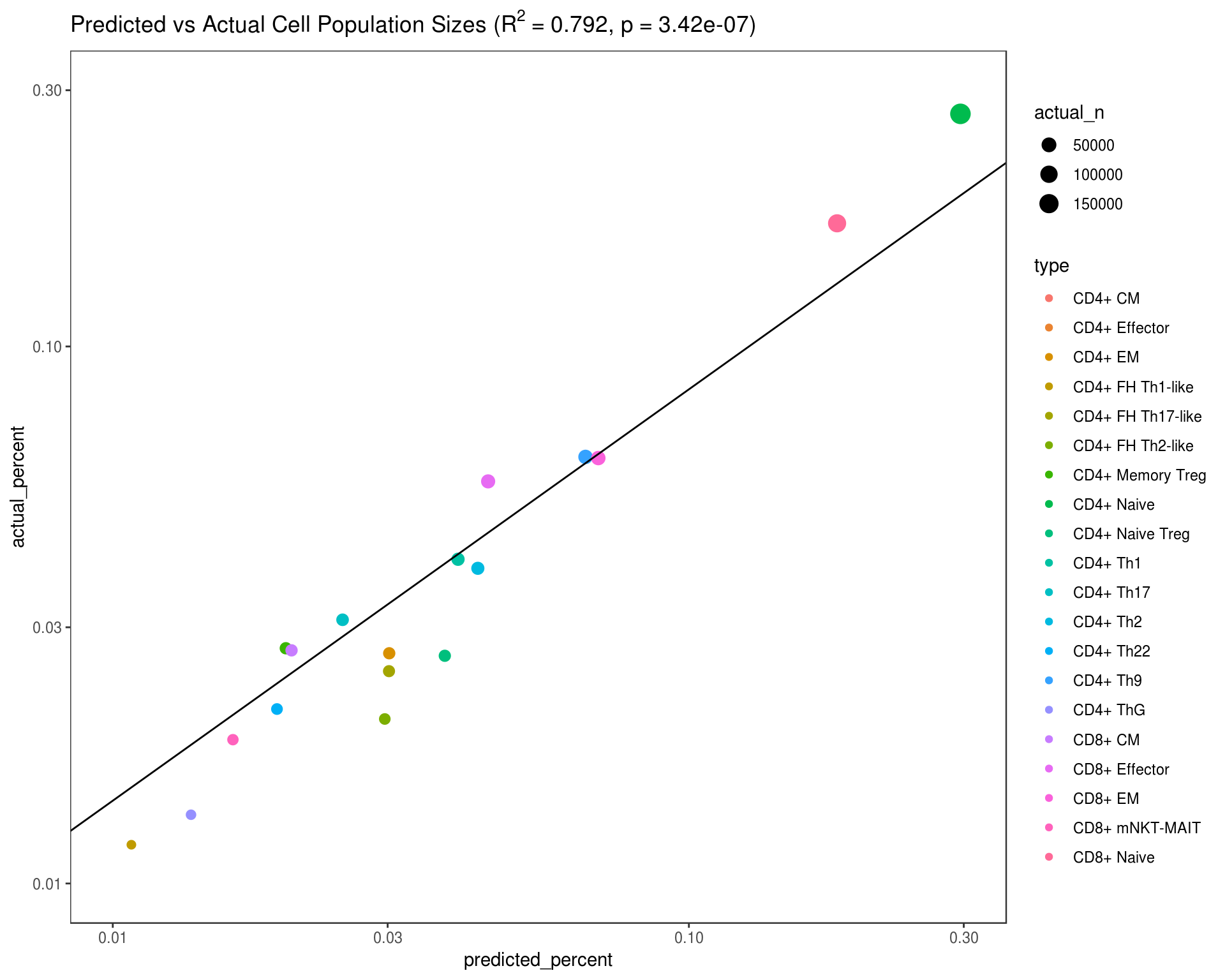

References

Givan, Alice L. 2010. “Flow Cytometry: An Introduction.” In Methods in Molecular Biology, 1–29.

Rowley, Tom. 2012. “Flow Cytometry - a Survey and the Basics.” MATER METHODS 2 (August).

Hahne, Florian, Nolwenn LeMeur, Ryan R Brinkman, Byron Ellis, Perry Haaland, Deepayan Sarkar, Josef Spidlen, Errol Strain, and Robert Gentleman. 2009. “FlowCore: A Bioconductor Package for High Throughput Flow Cytometry.” BMC Bioinformatics 10 (April): 106.

Shapiro, Howard M. 1994. Practical Flow Cytometry. Wiley-Liss.

Jaye, David L, Robert A Bray, Howard M Gebel, Wayne A C Harris, and Edmund K Waller. 2012. “Translational Applications of Flow Cytometry in Clinical Practice.” J. Immunol. 188 (10): 4715–9.

Aghaeepour, Nima, Greg Finak, FlowCAP Consortium, DREAM Consortium, Holger Hoos, Tim R Mosmann, Ryan Brinkman, Raphael Gottardo, and Richard H Scheuermann. 2013. “Critical Assessment of Automated Flow Cytometry Data Analysis Techniques.” Nat. Methods 10 (3): 228–38.

Bushnell, Tim. 2015. Modern Flow Cytometry. ebook.

Ortyn, William E, Brian E Hall, Thaddeus C George, Keith Frost, David A Basiji, David J Perry, Cathleen A Zimmerman, David Coder, and Philip J Morrissey. 2006. “Sensitivity Measurement and Compensation in Spectral Imaging.” Cytometry A 69 (8): 852–62.

Weber, Lukas M, and Mark D Robinson. 2016. “Comparison of Clustering Methods for High-Dimensional Single-Cell Flow and Mass Cytometry Data.” Cytometry A 89 (12): 1084–96.